Zachriel

Posts: 2723
Joined: Sep. 2006
|
| Quote (Bob O'H @ July 02 2009,13:52) | | I'm a bit cynical about a lot of conservation genetics: far too many people doing it use species of great conservation concern, like fruit flies. |
Heh. Then I suppose you are equally cavalier about the fate of isogenic yeast.
| Quote (Bob O'H @ July 02 2009,13:52) | | In think there has been some work showing it happens in nature, but there are so many other threats as well. |
When populations fall to very low levels, then minor catastrophes can result in extinction. With Gregor's Bookkeeper, if we set the relative variance to a high level (to represent contingent variations), then it can easily result in extinction. A low reproductive rate also makes a species less robust when populations are at a low level or subject to broad environmental fluctuations. Also important in very small populations is the role of recessive genes due to inbreeding. But in nature, we often expect some hybridization with closely related populations.
Some results of Gregor's Bookkeeper. Here are the settings for this trial.
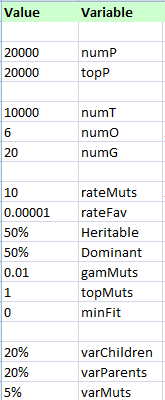
numP is number of Parents.
numT is the number of Turns (but was stopped).
numO is the average number of Offspring.
numG is the number of Genes.
Dominant of 50% has no effect.
(The limiting factor for the software seems to be the Roulette Selection algorithm. The above took a few hours. I may try to optimize it later or convert it to a C++ module—but I doubt it is worth the trouble.)
Even with the very low favorable-to-deleterious ratio of 0.00001, the result was an increase in fitness as seen here.
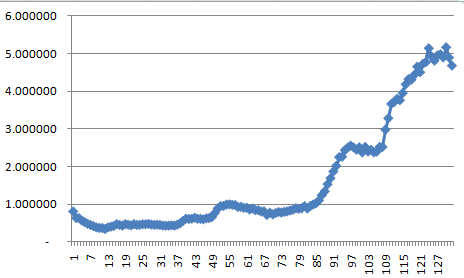
You can't see it well, but the fitness drops rapidly at the beginning. It's easier to see in log10.
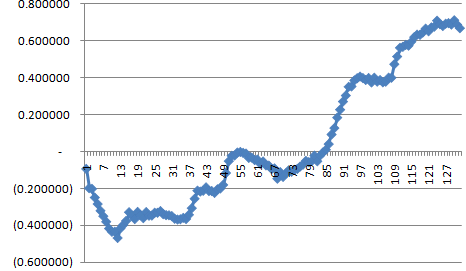
This is because the original population has a uniform (isogenic) fitness of 1, and it takes some time for it to stabilize as a population of nearly neutral mutations.
With a population of 100, it increases in fitness with a favorable-to-deleterious ratio of 0.001 0.002. With a population of 1000, it increases in fitness with a favorable-to-deleterious ratio of 0.0001 0.0002. In nature, a species of only a few thousand individuals is usually considered small.
One of the problems with the model is that {in nature} the ratio of favorable-to-deleterious tends to increase as fitness declines. But leaving that aside ... We see that with larger populations, and within the assumptions of the model, genetic meltdown is not an issue.
The "divide by random" selection algorithm in Mendel's Accountant is flawed. If we add a slight dominance to beneficial alleles or introduce sexual selection, the results would be even more lopsided. The conclusion that genetic meltdown is a problem for reasonably large populations, and that this sort of model indicates a problem for evolutionary theory, is not supported.
-
More accurate value reflects additional data.
--------------
You never step on the same tard twice—for it's not the same tard and you're not the same person.
|


















